手机赌钱这些极小值不仅在教师集上表现出较低的亏本-手机赌钱平台-登录入口

　　炒股就看金麒麟分析师研报，泰斗，专科，实时，全面，助您挖掘后劲主题契机！

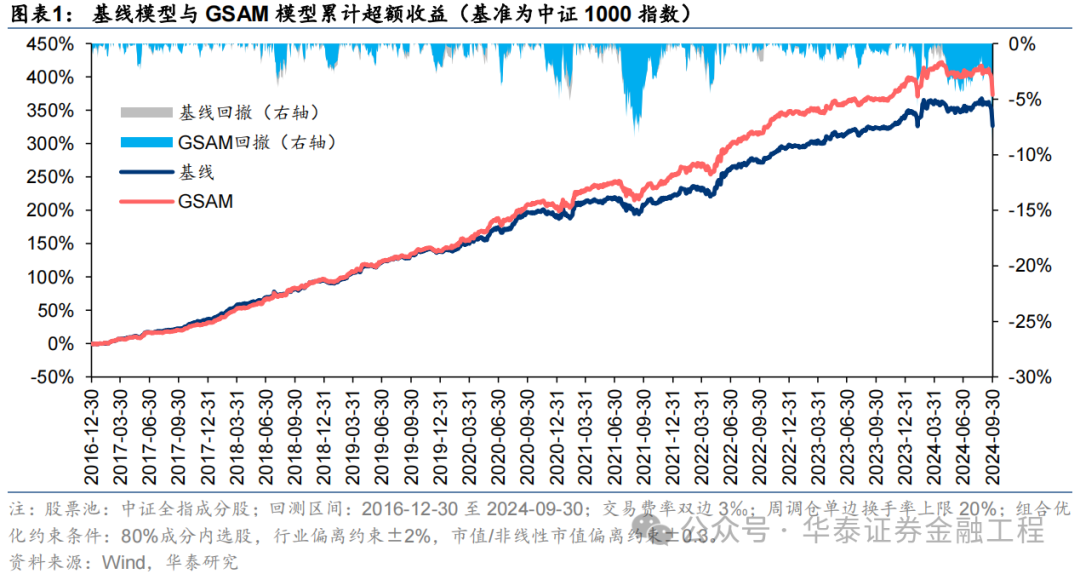
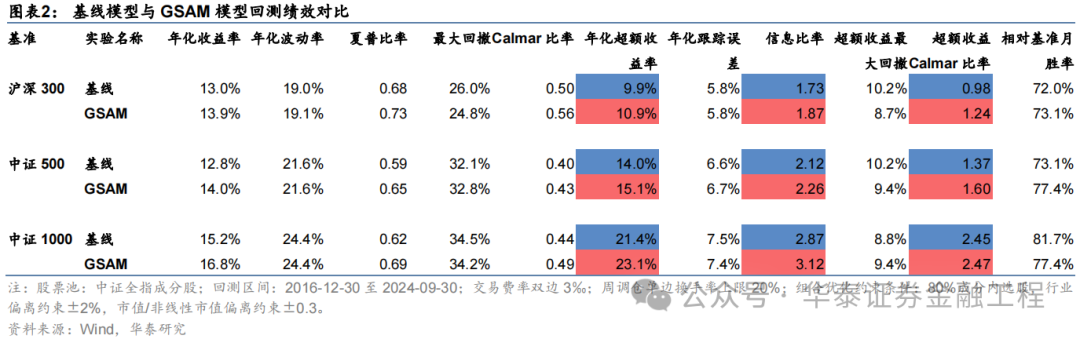
本辩论先容一种低资本、高通用性的正则化步伐——Sharpness Aware Minimization（SAM），从优化器的角度栽培模子的泛化性能。在GRU基线模子的基础上，采用传统优化器AdamW、SAM优化器偏执四种创新版块进行对信得过验。扫尾标明应用SAM优化器能显赫栽培模子预计因子的多头端收益，且基于各种SAM模子构建的指数增强组合功绩均显赫优于基线模子。其中，GSAM模子在三组指数增强组合上均得回高超表现，沪深300、中证500和中证1000增强组合年化逾额收益永别为10.9%、15.1%和23.1%，信息比率永别为1.87、2.26和3.12，显赫优于基线模子，而ASAM模子2024年表现凸起，三组指数增强组合逾额收益均首先基线模子约5pct。

中枢不雅点

]article_adlist-->

东谈主工智能84：应用SAM优化器栽培AI量化模子的泛化性能

SAM优化器通过追求“平坦极小值”，增强模子鲁棒性

SGD、Adam等传统优化器进行梯度下跌时仅以最小化亏本函数值为方针，易落入“浓烈极小值”，导致模子对输入数据散播敏锐度高，泛化性能较差。SAM优化器将亏本函数的平坦度加入优化方针，不仅最小化亏本函数值，同期最小化模子权要点隔邻亏本函数的变化幅度，使优化后模子权重处于一个平坦的极小值处，加多了模子的鲁棒性。基于SAM优化器，ASAM、GSAM等创新算法被陆续建议，从参数圭臬自适合性、扰动标的的准确性等方面进一步增强了SAM优化器的性能。

SAM优化器能镌汰教师过程中的过拟合，栽培模子的泛化性能

SAM优化器想象初志是使模子教师时在权重空间中找到一条简易的旅途进行梯度下跌，改善模子权重空间的平坦度。可通过不雅察模子教师过程中评价方针的变化趋势以及亏本函数地形图对其进行考据。从评价方针的变化趋势分析，SAM模子在考据集上IC、IR方针下跌幅度较缓，教师过程中评价方针最大值均高于基线模子；从亏本函数地形分析，SAM模子在教师集上亏本函数地形相较基线模子愈加平坦，测试集上亏本函数值举座更低。抽象两者，SAM优化器能有用欺压教师过程中的过拟合，栽培模子的泛化性能。

SAM优化器能显赫栽培AI量化模子表现

本辩论基于GRU模子，对比AdamW优化器与各种SAM优化器模子表现。从预计因子表现看，SAM优化器能栽培因子多头收益；从指数增强组合功绩看，SAM模子偏执创新版块模子在三组指数增强组合功绩均显赫优于基线模子。2016-12-30至2024-09-30内，抽象表现最好模子为GSAM模子，单因子回测TOP层年化收益高于31%，沪深300、中证500和中证1000增强组合年化逾额收益永别为10.9%、15.1%和23.1%，信息比率永别为1.87、2.26和3.12，显赫优于基线模子。2024年以来ASAM模子表现凸起，三组指数增强组合逾额收益均首先基线模子约5 pct。

正文

]article_adlist-->

01 导读

栽培泛化性能是增强AI量化模子表现的要害。对AI量化模子应用适当的正则化步伐，不错进一步“强化”模子，栽培其泛化性能，让量化战略的表现更进一步。正则化步伐的方针为开拓模子捕捉数据背后的广泛轨则，而不是单纯地牵记数据样本，从而栽培模子的泛化性能。正则化步伐种类繁密，其通过纠正亏本函数或优化器、造反教师、扩凑数据集、集成模子等技能，使模子教师过程愈加矜重，幸免模子对教师数据的过拟合。

本辩论先容一种低资本、高通用性的正则化步伐Sharpness Aware Minimization（SAM），从优化器的角度栽培模子的泛化性能。该步伐对传统优化器梯度下跌的算法进行创新，建议了鲁棒性更强的SAM优化器，通过寻找权重空间内的“平坦极小值”，使模子不仅在教师集上表现高超，且在样本外相似表现雄厚。SAM优化器建议后，学术界陆续迭代出了各种创新的SAM优化器，从不同角度进一步增强SAM优化器的表现。

本辩论在GRU模子的基础上应用SAM优化器偏执各种创新版块进行实验，扫尾标明：

SAM优化器相较于传统优化器在模子教师过程中考据集上过拟合速率镌汰，且亏本函数曲面平坦度栽培，展现出更强的泛化性能；

SAM优化器偏执创新版块教师模子预计因子2016-12-30至2024-09-30内多头组年化收益31.4%，相较于等权基准信息比率4.0，比较基线模子栽培显赫；

应用SAM优化器偏执创新版块教师模子构建指数增强组合，相较于GRU基线模子栽培显赫，沪深300、中证500、中证1000指数增强组合逾额收益栽培在1-2 pct；

对比各SAM优化器教师模子表现，回测全区间内GSAM模子预计因子方针及指增组合功绩方针表现较好，ASAM模子2024年以来表现凸起。

02SAM优化器与模子泛化性能

正则化步伐

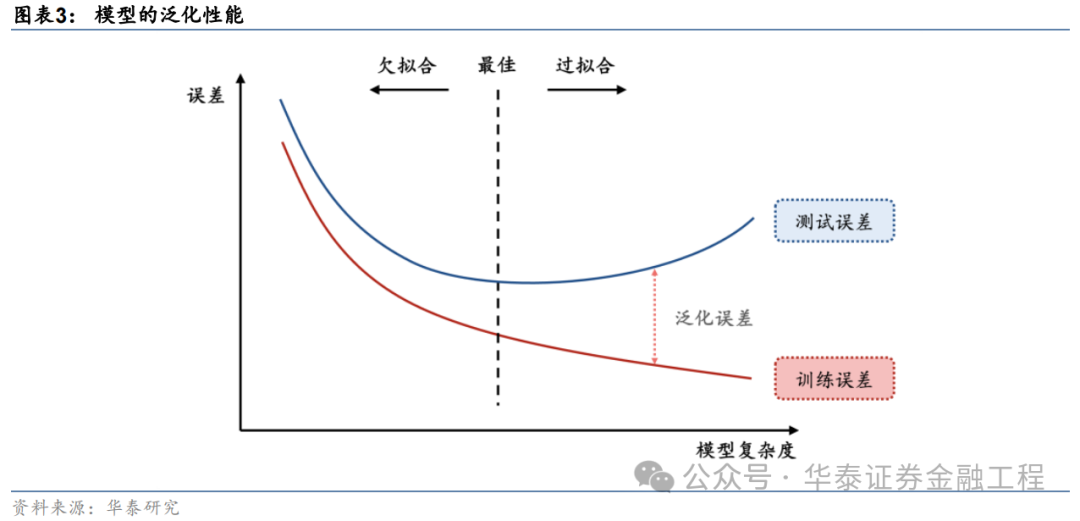
正则化步伐（regularization）旨在使模子变得“更粗略”，退缩过拟合。机器学习中的一个要害挑战是让模子大概准确预计未见过的数据，而不单是是在纯属的教师数据上表现高超，即镌汰模子的泛化舛讹。正则化的方针是饱读动模子学习数据中的芜俚模式，而不单是记着数据本人。正则化步伐通过各种技能，使教师后的模子处于最好景色，在教师数据和测试数据上得回相似高超的表现。

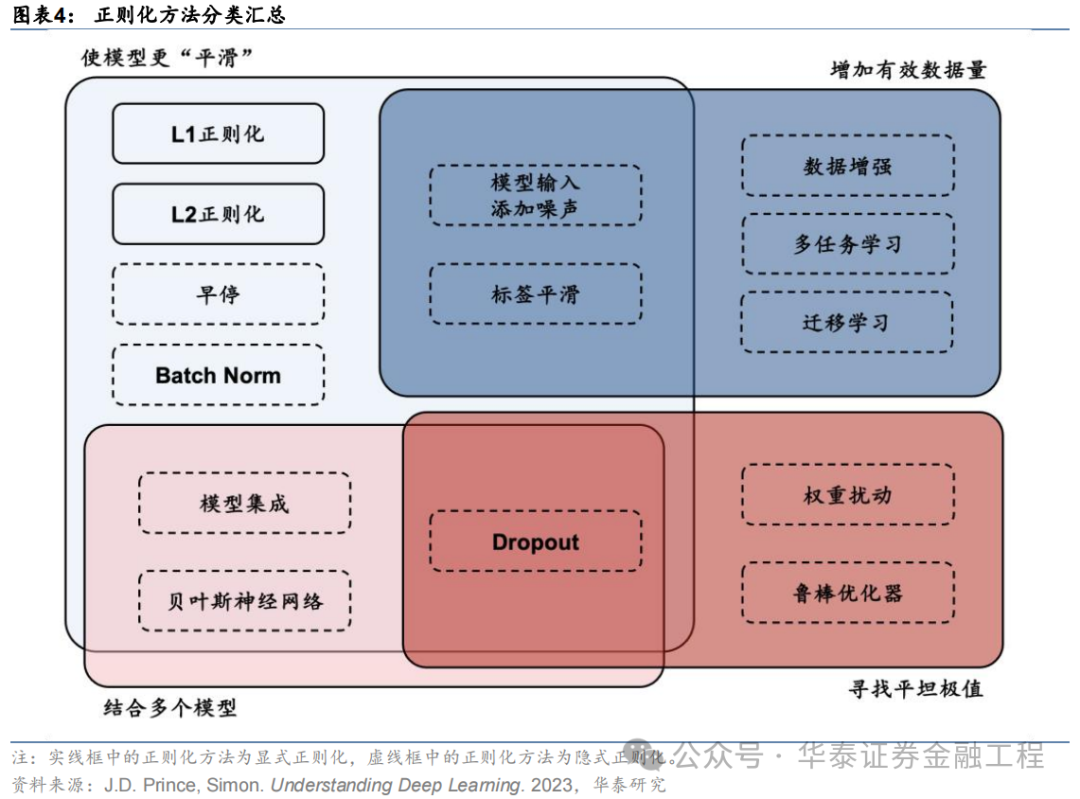
正则化步伐的体式各种。其中狭义的正则化往往指显式正则化步伐，即在亏本函数中显式添加一个刑事职守项或经管，镌汰模子的复杂性，典型的显式正则化项包括L1、L2正则化；而广义的正则化往往指隐式正则化，其含义较为芜俚，在当代机器学习步伐中无处不在，包括早停、Dropout、数据增强、去极值、多任务学习、模子集成等，实在统统发奋于于增强模子泛化性能的步伐齐可归于此类。

传统优化器偏执局限性

深度学习范畴中，优化器的选拔关于模子教师的效用和最终性能至关遑急。在广漠优化算法中，立地梯度下跌（SGD）偏执变体是最为基础且芜俚使用的优化步伐之一。SGD通过逐次或批量更新权重来最小化亏本函数，尽管粗略有用，但其学习率的选拔和漂泊问题是主要局限。为了克服这些问题，Adagrad、RMSprop以及Adam等优化器被陆续建议，有用栽培了SGD优化器适用性和性能。下表汇总了深度学习中常用的传统优化器的脾气和局限性。

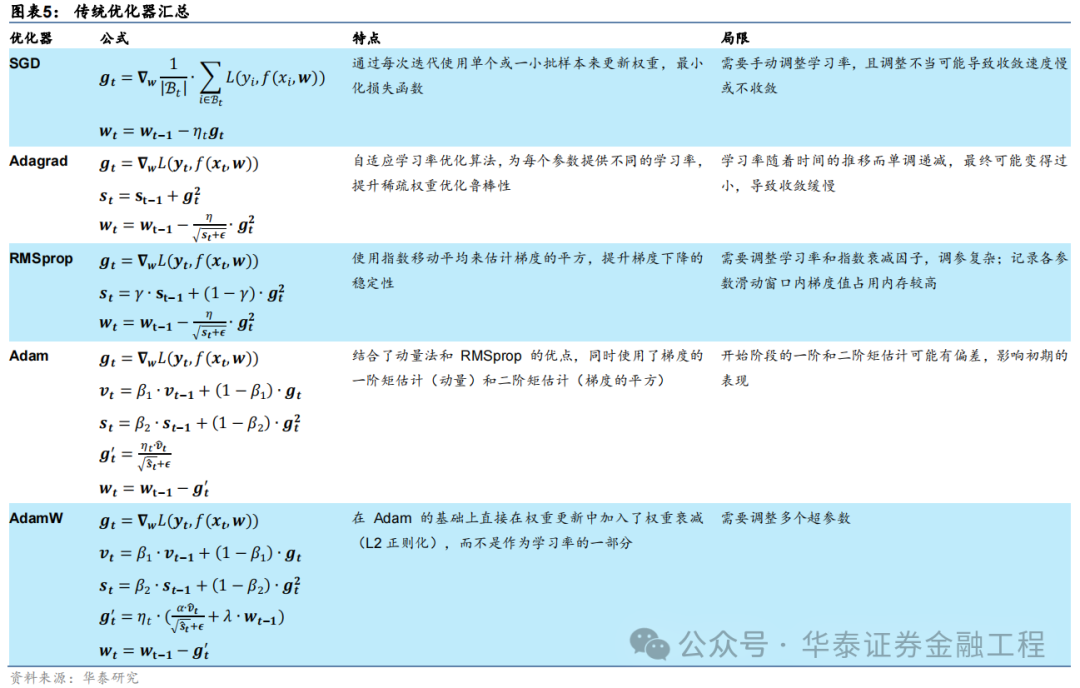
除了以上汇总的优障碍，传统的优化器比较本文先容的SAM优化器还有一个共同的局限：传统优化器往往只研讨最小化教师集上的亏本函数，可能堕入“浓烈极小值”，这些极小值点处诚然教师亏本较低，但经常会导致过拟合风光，即模子对教师数据过度拟合而泛化性能较差。比较之下，SAM优化算法大概克服这些局限性，在教师时寻找“平坦极小值”，这些极小值不仅在教师集上表现出较低的亏本，况兼在测试集上也具有较好的泛化性能。

Sharpness Aware Minimization

Sharpness Aware Minimization（SAM）步伐最初由Google Research团队Foret等东谈主（2021）建议。该步伐的起点为对模子进行优化时，不仅但愿优化后的模子权重所处位置亏本函数较小，同期还但愿该位置在模子权重空间中亏本函数的“地形”较为平坦。由此扩充出三个问题：什么是亏本函数“地形”？为什么平坦的极值点处模子的泛化性能较优？若何追求平坦的极值点？

什么是亏本函数“地形”？

亏本函数地形即亏本函数值与模子参数之间的变化关系。在优化问题中，亏本函数可看作以模子参数为自变量的函数，用公式浮现即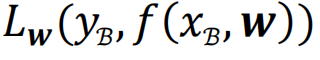

。关于神经收罗这类具有广泛参数的模子，自变量为一个高维向量。若分歧模子参数进行降维处理，则亏本函数地形为高维空间中的一个曲面，曲面上的每一个点代表一组自变量取值时的亏本函数值。

由于高维空间亏本函数曲面难以可视化，当作辩论对象不够直不雅，因此往往可对模子参数降维，通过简化后的低维空间进行可视化和解析。例如来说，假设模子中唯惟一个可变参数，则此时亏本函数地形即退化为一维的亏本函数弧线；相似假设从高维模子参数中提真金不怕火两个主要重量当作模子参数，即可将亏本函数与参数之间的变化关系用二维曲面进行浮现，这亦然最为常见的作念法。

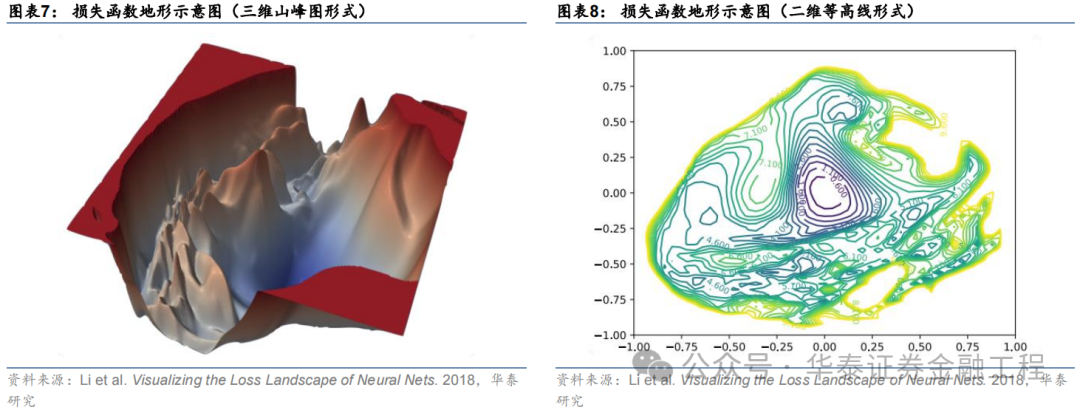
为什么平坦的极值点处模子的泛化性能较优？

以一维亏本函数弧线为例进行证据。下图展示了两个款式不同的极值点，其中左边的极值点较为“平坦”，即亏本函数跟着模子参数的变化较小，而右边“浓烈”的极值点则相悖。若模子教师完成后处于右边的“浓烈”极值点，诚然其在教师数据上的亏本函数值较小，但当模子在测试数据上进行施行预计时，由于测试数据与教师数据之间散播的偏差，预计扫尾将会产生较大舛讹。而若模子教师完成后处于左边的“平坦”极值点，则测试数据与教师数据的偏差给模子预计带来的影响就相对微弱。

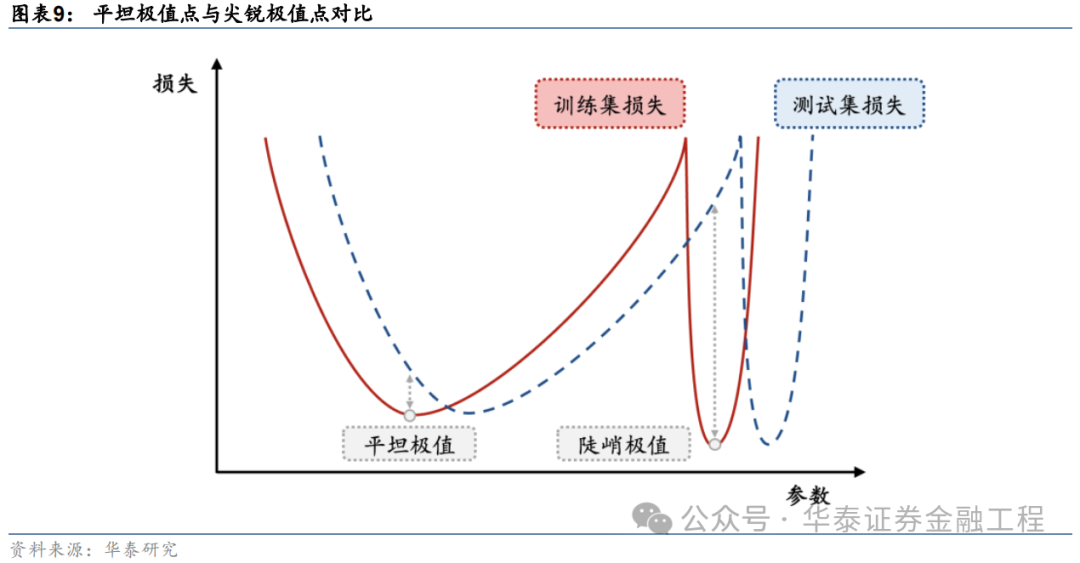
若何追求平坦的极值点？

SAM优化器通过两次梯度下跌，微调梯度下跌的标的来寻找权重空间中较为平坦的极值点。具体作念法为：将传统的优化器的优化方针从优化一个权要点位置处的亏本函数改为优化这个点以偏执扰动领域内全部点亏本函数的最大值。用公式抒发即：

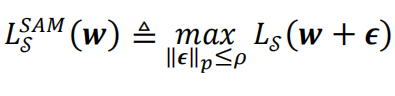
其中]article_adlist-->代表优化的方针函数，]article_adlist-->代表模子权重，而]article_adlist-->则代表权要点]article_adlist-->隔邻的一个微弱扰动值，]article_adlist-->为落幕该扰动值大小的超参数。

而某权要点扰动领域内亏本函数最大值的位置其实是已知的。惯例优化算法梯度下跌时沿着该权要点处亏本函数的负梯度方上前进，可使亏本函数最速下跌。因此，亏本函数最大值的位置的标的即亏本函数的正梯度标的。在该权要点处沿着亏本函数正梯度方上前进一小步的位置即扰动领域内亏本函数最大值处。用公式抒发即：

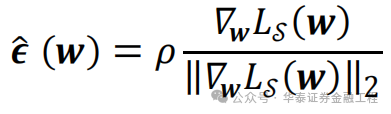
其中，]article_adlist-->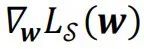

为亏本函数]article_adlist-->在]article_adlist-->处的梯度，而分母中的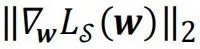

则浮现该梯度张量的二阶模。

浮现的便是亏本函数高潮最快的扰动标的，

将]article_adlist-->

代入

中并求梯度，经过泰勒伸开及近似，就不错得到SAM优化算法在教师时每一步施行更新的梯度：

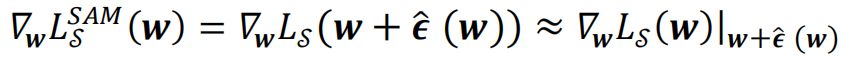
即在SAM算法中，

每一次梯度下跌时用亏本函数]article_adlist-->在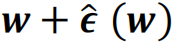

处的梯度更新点处的模子权重

。

]article_adlist-->

SAM优化器算法经由浮现图和伪代码如下图所示。

SAM优化器的创新

SAM优化器也曾建议即在学术界引起了芜俚眷注。SAM优化器通过爽直有用的算法逻辑增强了模子的泛化性能，但相似也存在多方面的创新空间。很多创新版块的SAM优化器被陆续建议，汇总如下：

对SAM优化器的创新主要分为两个标的，永别注释优化SAM优化器的性能和效用。关于应用于量化选股的AI模子而言，优化器的泛化性能才是最终决定模子预计成果的因素，因此优化器的效用相较于其性能并不要害。接下来简要先容着眼于创新性能的几种创新SAM优化器。

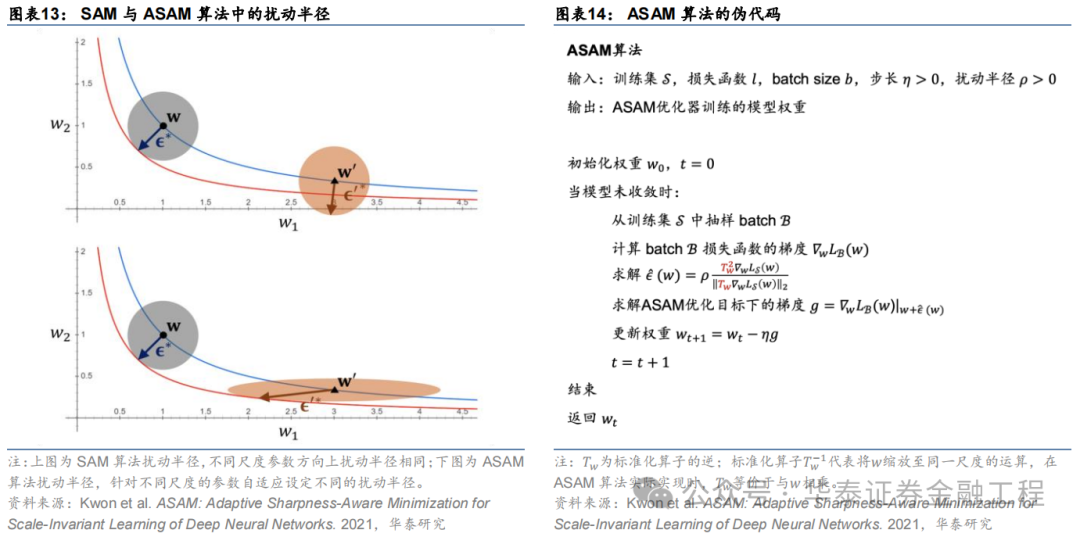
ASAM

Adaptive Sharpness Aware Minimization（ASAM）由Kwon等（2021）建议。ASAM优化器相较于SAM优化器的创新近似于Adagrad优化器相较于SGD优化器的创新，区别在于后者调养学习率大小以适合神经收罗中不同参数的圭臬，而前者调养权重空间内扰动半径以适合神经收罗中不同参数的圭臬。ASAM优化器引入了自适合扰动半径的见地，在野心权重空间内扰动半径时研讨到各参数的圭臬，因此通过该步伐野心得到的SAM优化旅途与各参数本人的圭臬无关，惩处了SAM中锐度界说的敏锐性问题，提高了模子的泛化性能。

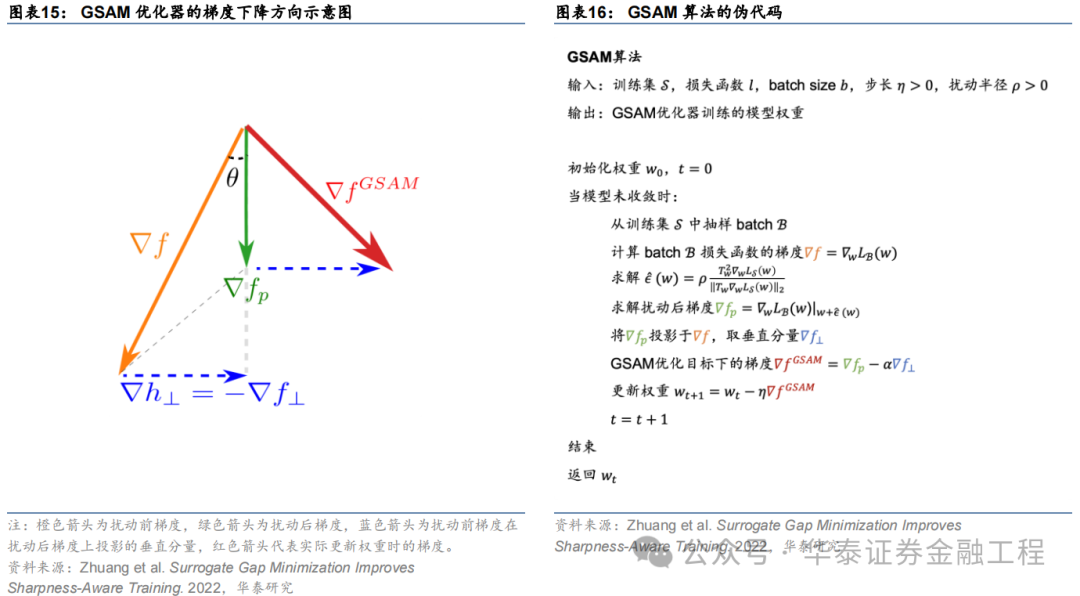
GSAM

Surrogate Gap Guided Sharpness Aware Minimization（GSAM）由Zhuang等（2022）建议。该辩论发现扰动后亏本与扰动前亏本之差（即surrogate gap）更能准确预计模子权重空间极小值处亏本地形的平坦度。由此进一步推导出GSAM优化器的梯度更新步伐：第一步近似于SAM，通过梯度下跌最小化扰动亏本；第二步则在施行更新权重时首先将扰动前梯度在扰动后梯度方朝上投影得到垂直重量，接着将扰动后梯度与该垂直标的重量相加得到最终梯度下跌的标的，更新模子权重。

GAM

Gradient Norm Aware Minimization（GAM）由Zhang等（2023）建议。本辩论发现，应用SAM步伐时往往因为小区域内存在多个极值点的情形导致“误判”：即使在小扰动半径内亏本函数波动至极剧烈，但因为扰动后参数点的亏本函数与扰动前差距较小而以为在该扰动领域内亏本函数是“平坦”的。因此，GAM步伐通过同期优化扰动半径内的零阶平坦度（亏本函数平坦度）以及一阶平坦度（梯度平坦度）幸免了该种“误判”。

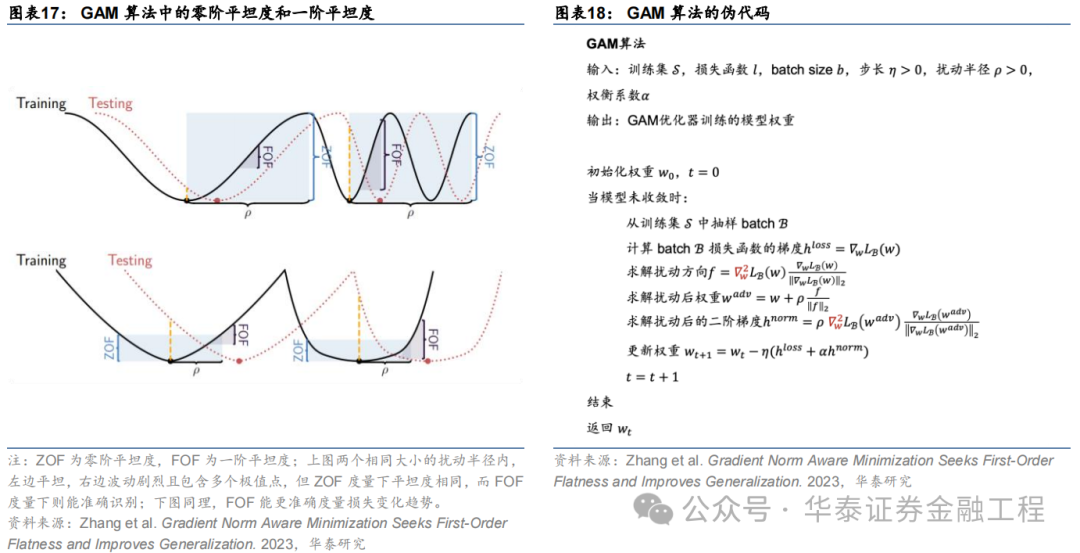
FSAM

Friendly Sharpness Aware Minimization（FSAM）由Li等（2024）建议。辩论发现SAM优化器的扰动标的不错被阐明为全梯度重量和仅与每个小批量相关的立地梯度噪声重量，且前者对泛化性能的有显赫的负面影响。FSAM优化器通过指数迁徙平均（EMA）揣度扰动标的中的全梯度重量，并将其从扰动向量中剥离，仅利用立地梯度噪声重量当作扰动向量，成效减少了全梯度身分对泛化性能的负面影响，从而提高了模子的泛化性能。

03实验步伐

基线模子

本辩论基于端到端的GRU量价因子挖掘模子测试SAM优化器的创新成果。基线模子的构建步伐如下图，永别使用两个GRU模子从日K线和周K线中提真金不怕火特征得到预计值，当作单因子，再将两个单因子等权合成得到最终的预计信号。GRU模子的构建细节可参考《神经收罗多频率因子挖掘模子》（2023-05-11），本文不作念伸开。

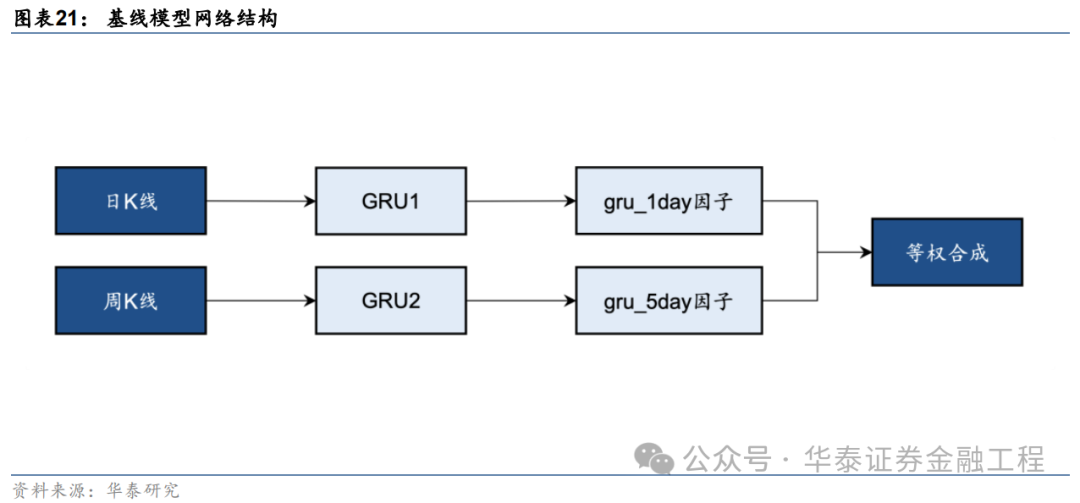
基线模子输入数据细节及教师超参数建立如下表：

SAM优化器

SAM优化器的凸起脾气即适用性强，吞并种SAM优化器大概封装各种不同的基础优化器，而无需对模子教师的经由进行大领域的修改。本辩论将SAM优化器应用于基线模子，GRU的收罗结构及超参数均不作念编削，仅编削模子教师时使用的优化器。其中，SAM优化器偏执4种创新版块均中式AdamW当作基础优化器，优化器的学习率、动量和权重衰减等超参数均不作念调养。5组对比实验采用的SAM优化器偏执独到参数取值汇总如下。

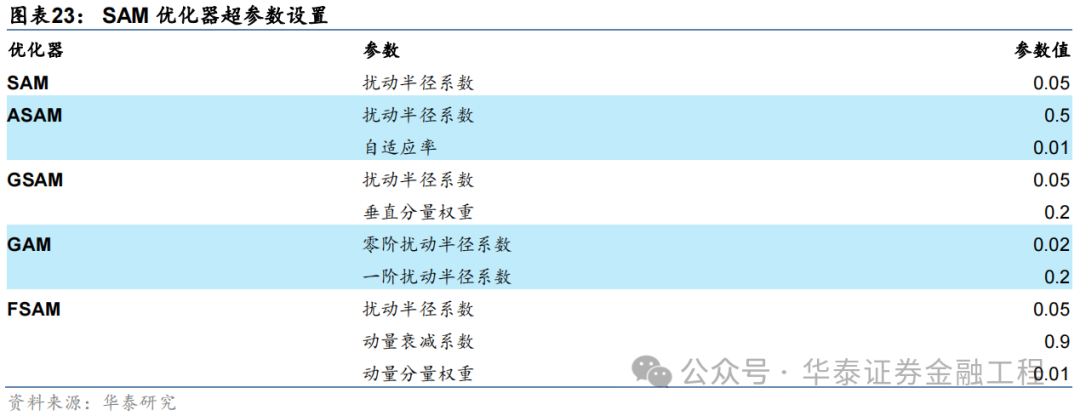
04 实验扫尾

本辩论在GRU基线模子的基础上，保捏模子结构、数据集不变，编削教师使用的优化器共进行6组对比实验。以下永别从模子教师时的经管性、亏本函数地形、模子预计因子表现和基于模子构建指数增强组合功绩等方面展示实验扫尾。

模子经管性

模子教师过程中亏本函数和评价方针在考据集上表现的变化趋势是模子泛化性能最直不雅的体现。若教师时跟着Epoch加多，考据集的评价方针旋即栽培后赶紧下跌，则证据模子过拟合严重，泛化性能欠安；反之，若考据集的评价方针跟着Epoch加多矜重栽培，则证据模子泛化性能较好。

本节中式交流种子点、交流数据集下的基线模子与SAM模子，对比教师过程中两者在考据集上IC、IR等方针的变化趋势。

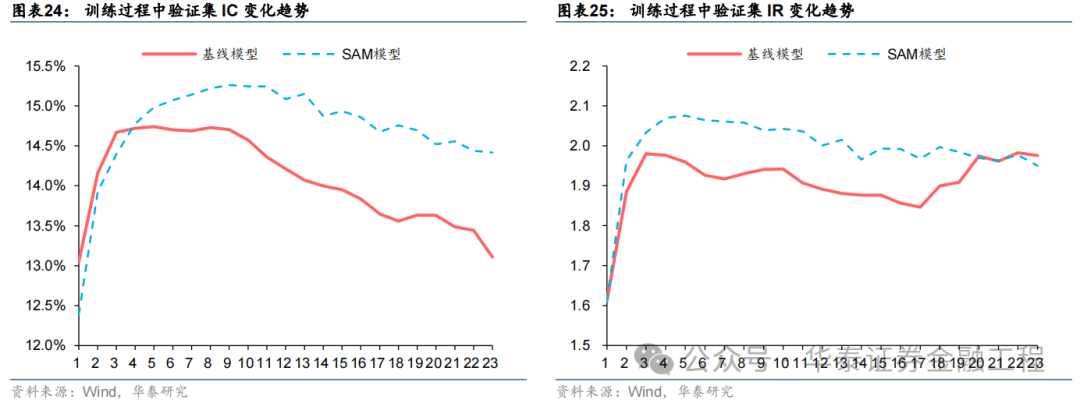
扫尾标明，基线模子与SAM模子在考据集上IC、IR方针变化趋势均为先高潮后下跌，但相较而言，SAM模子下跌幅度较缓，且教师过程中方针最大值均高于基线模子，解说SAM优化器有用欺压了过拟合，栽培了模子的泛化性能。

亏本函数地形

SAM优化器想象初志是使模子教师时在权重空间中找到一条简易的旅途进行梯度下跌，即每次权重更新时亏本函数不剧烈变化，最终在权重空间中停留在一个平坦的极值点处。因此，本节尝试对模子权重空间上的亏本函数进行可视化，以教师SAM优化器的应用成果。

轮回神经收罗的权重往往包含斗量车载的参数，以GRU为例，输入时序维度为30、掩蔽层维度为64、特征数为6、层数为2的收罗共包含40000多个权重参数，每次梯度下跌时，优化器同期对统统参数迭代更新。因此，可视化一个数万维度权重空间上的亏本函数值并非易事。常见的惩处步伐为通过PCA、t-SNE等技艺将高维空间的权重降维至二维或三维，从而绘图一幅亏本函数“地形图”。

本辩论采用PCA步伐，绘图亏本函数“地形图”，具体程序如下：

中式教师轨迹上考据集最优权重当作原点；

对教师轨迹上的统统权重向量哄骗主身分分析，从中提真金不怕火出两个主身分向量，永别当作二维图像的两个轴标的；

生成一组二维龙套点阵当作图像每个像素点的坐标，并对每个坐标点对应的神经收罗权重在给定数据集上使用全部样本进行一次推理，野心亏本函数值，当作该点的像素值。该程序完成后即可绘图出一张二维的亏本函数地形图像；

将模子教师时每个Epoch的模子权重投影至该二维平面，结束模子教师轨迹的可视化。

依据该步伐，本文中式基线模子与SAM模子，在交流数据集和交流的立地数种子点的前提下，永别绘图亏本函数地形图。绘图时对两组实验永别中式主身分轴，并采用交流的亏本函数等高线和交流的像素分辨率，永别绘图教师集和测试集上的亏本函数地形，扫尾如下：

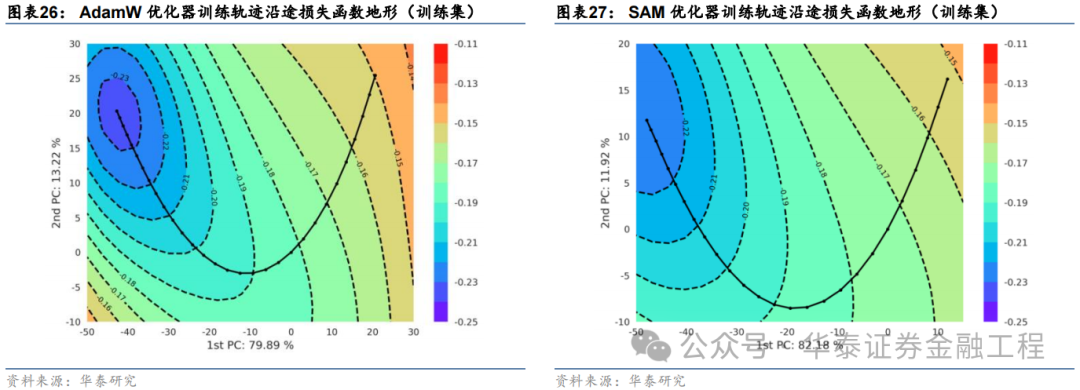
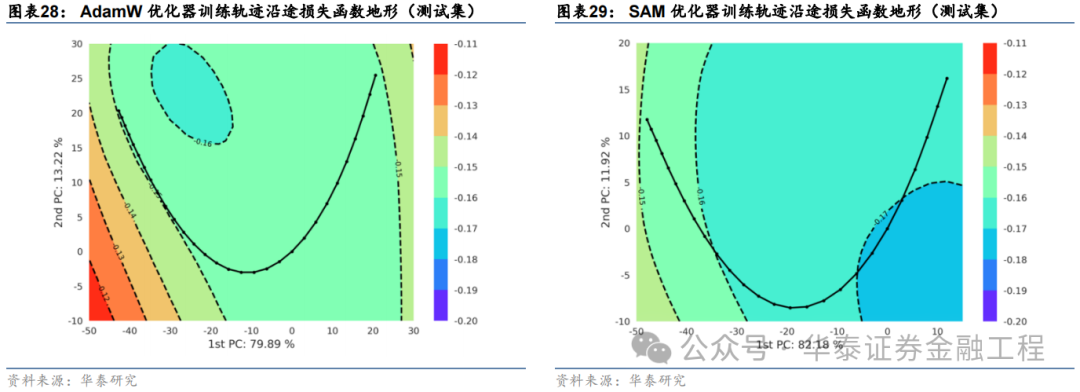
对比以上扫尾发现：

两组实验的第一主身分轴均达到80%驾驭的方差孝敬率，且两个主身分轴的累计孝敬率均首先了90%，证据两幅亏本函数曲面图均能很好的响应教师轨迹一谈亏本函数的变化趋势；

教师集上基线模子亏本函数地形图等高线较为密集，而SAM模子亏本函数地形图等高线较为稀疏且散播均匀，证据SAM优化器能有用改善亏本地形的平坦度，适当预期；

SAM模子在测试集上的亏本函数地形与基线模子比较举座亏本函数值较低，其中SAM模子早停处亏本函数值小于-0.17，而基线模子早停处亏本函数值大于-0.16，证据SAM模子泛化舛讹较小，即在教师数据与测试数据上表现相似高超，有用欺压了过拟合。

因子表现

针对6组实验，永别测试模子预计因子表现。单因子测试的细节如下：

测试扫尾如下，可得出如下论断：

SAM模子与基线模子预计因子RankIC及RankICIR表现接近，标明将传统优化器改为SAM优化器并未显赫栽培模子预计因子的RankIC表现；

5组SAM模子TOP组收益率均高于基线模子，其中GAM、GSAM、FSAM组栽培较为明显，FSAM模子表现最好。解说应用SAM优化器能有用改善预计因子多头端预计准确性，栽培多头组表现；

几组实验预计因子分层成果均较为优异，多头端收益5组SAM优化器模子广泛高于基线模子。

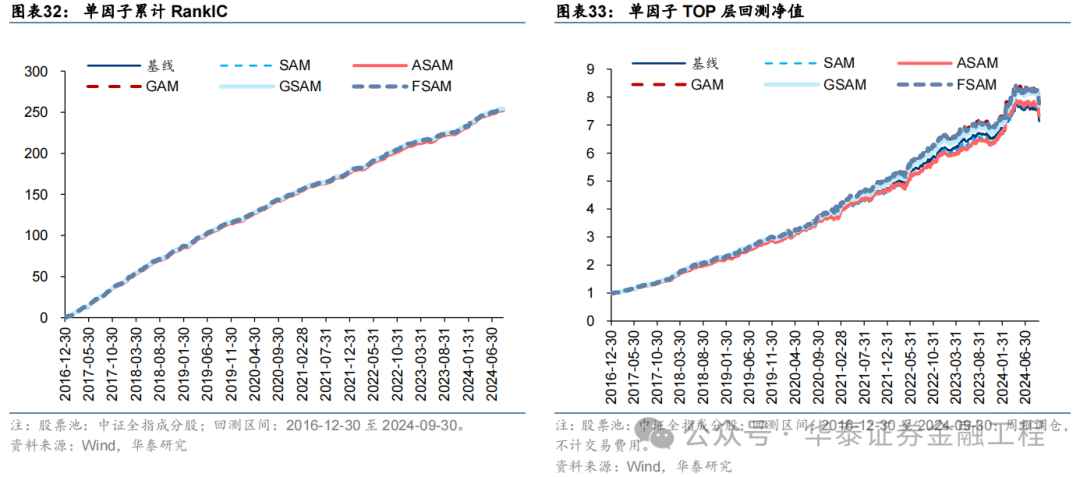
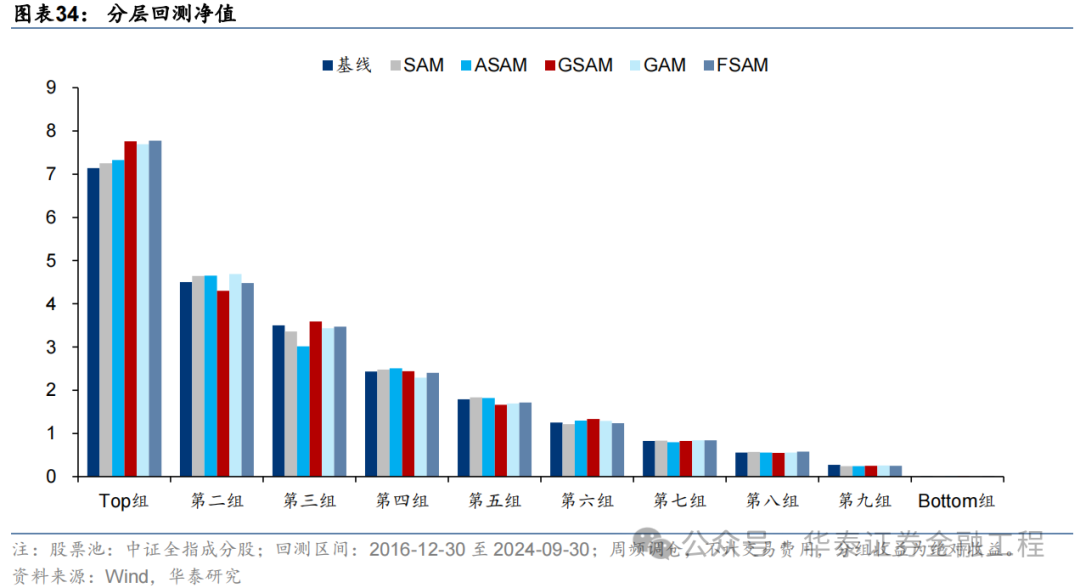
指数增强组合表现

将以上6组实验得到的预计因子应用于组合优化，永别构建沪深300、中证500及中证1000指数增强组合。组合优化及回测细节如下。

沪深300增强组合

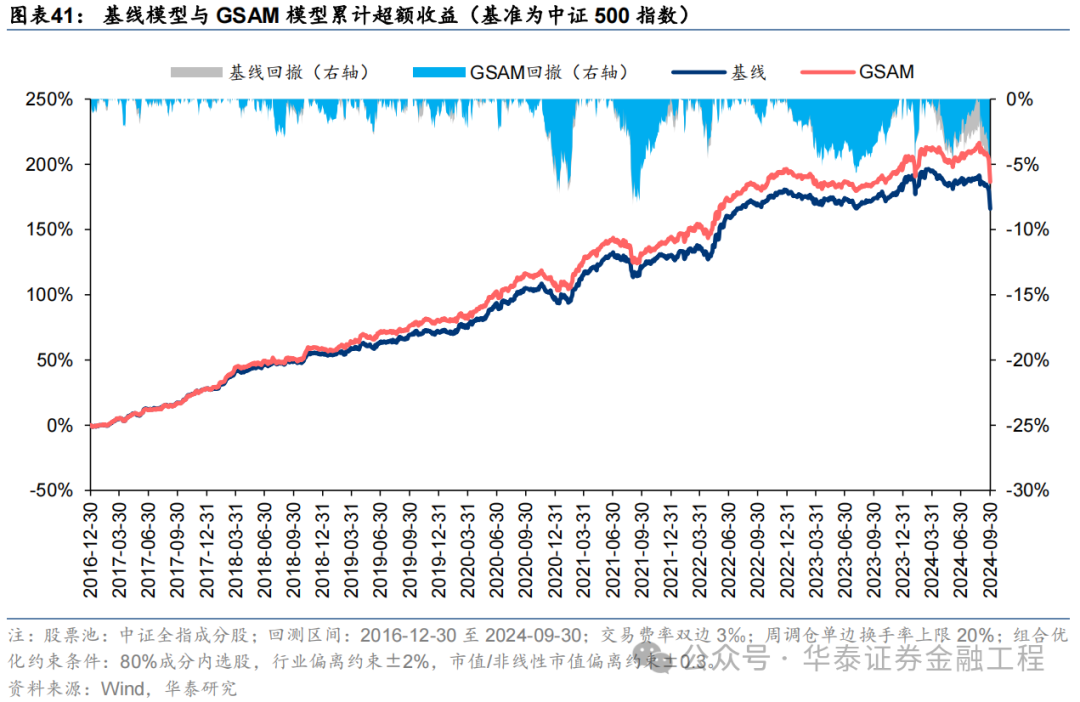
基于6组实验预计因子构建的沪深300指数增强组合回测扫尾如下。测试扫尾标明，SAM模子及4个创新模子年化逾额收益及信息比率相较于基线模子均有雄厚栽培。其中GSAM模子表现最好，年化逾额收益、信息比率、逾额收益Calmar比率及胜率在几组实验中均排行第一。

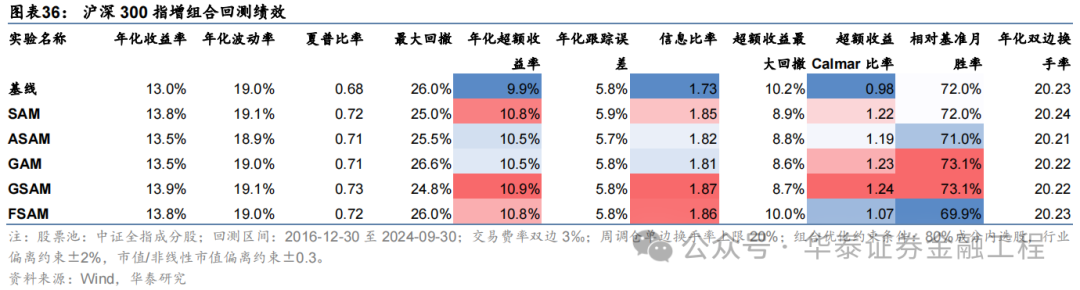
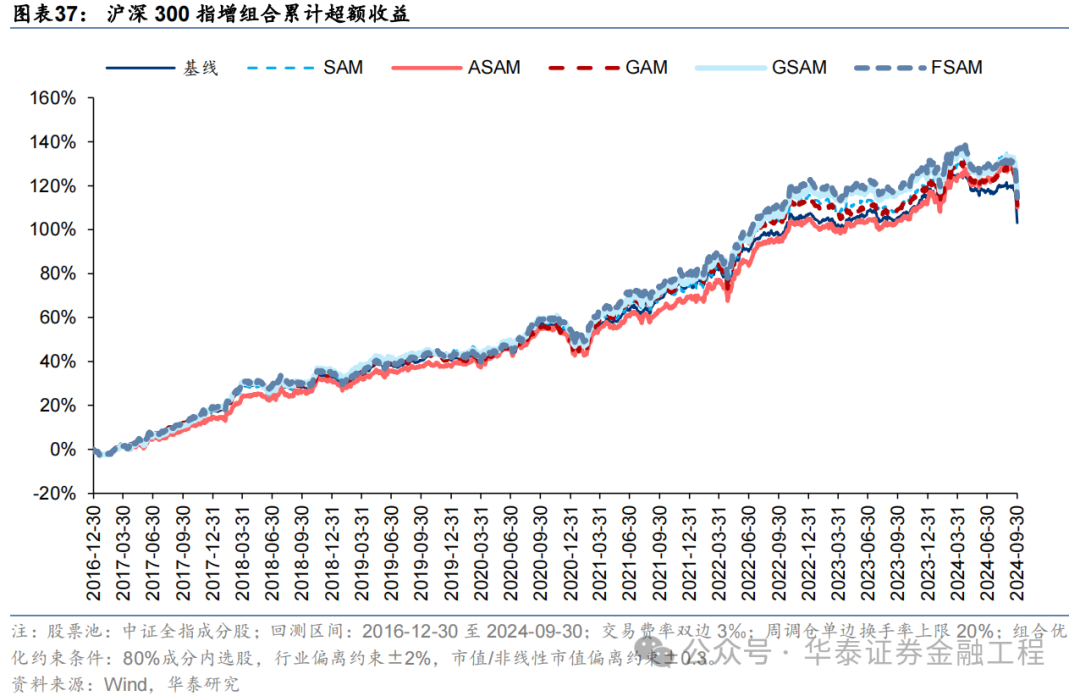
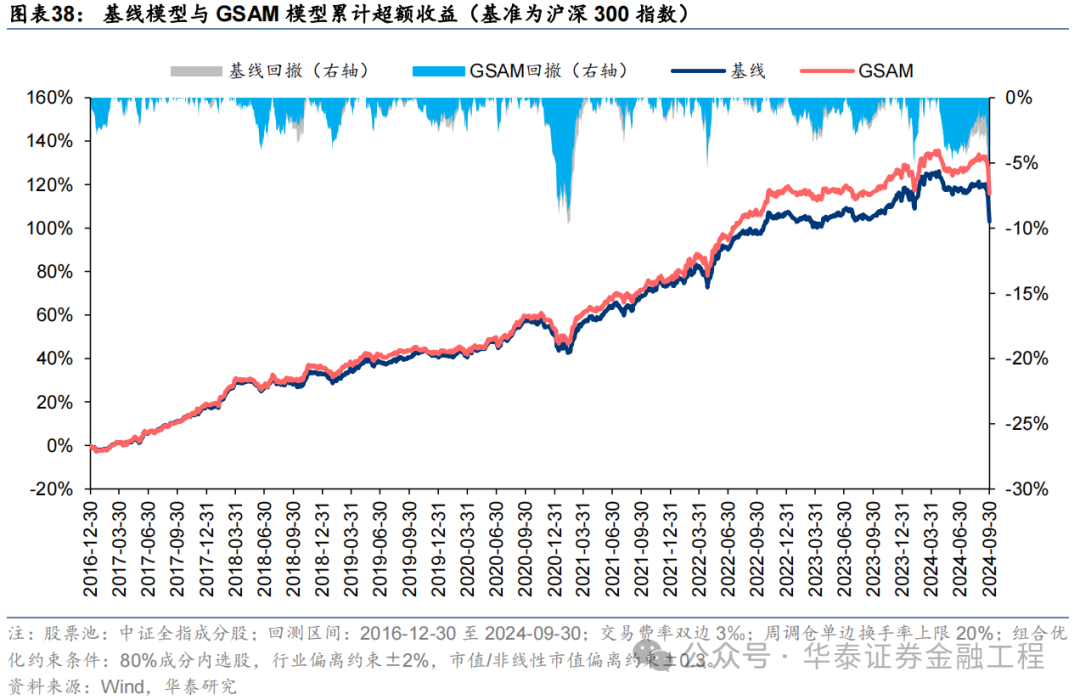
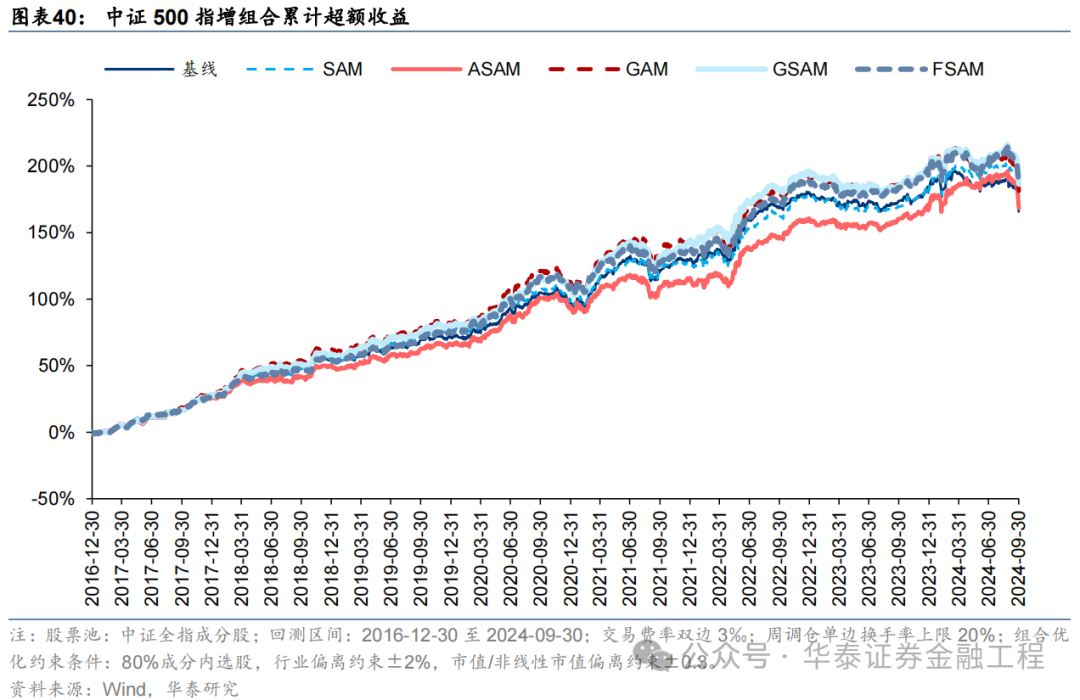
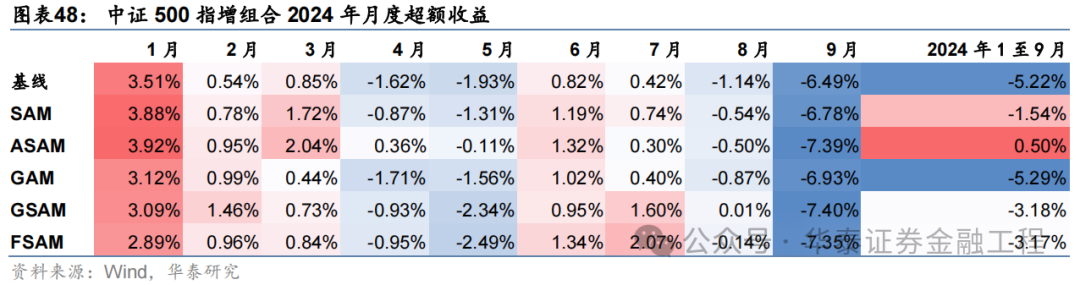
中证500增强组合

基于6组实验预计因子构建的中证500指数增强组合回测扫尾如下。测试论断与沪深300近似，GSAM模子年化逾额最高为15.1%，FSAM模子信息比率最高为2.29。另外，除了GAM模子外，其余模子在回撤落幕和月度胜率方面相较于基线模子也相似具有上风。

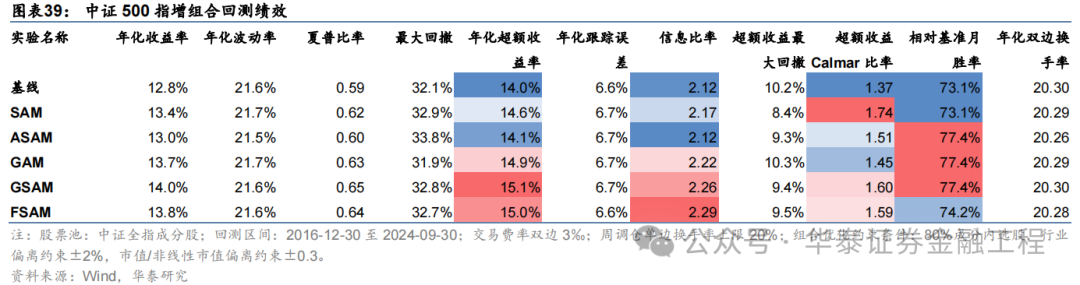
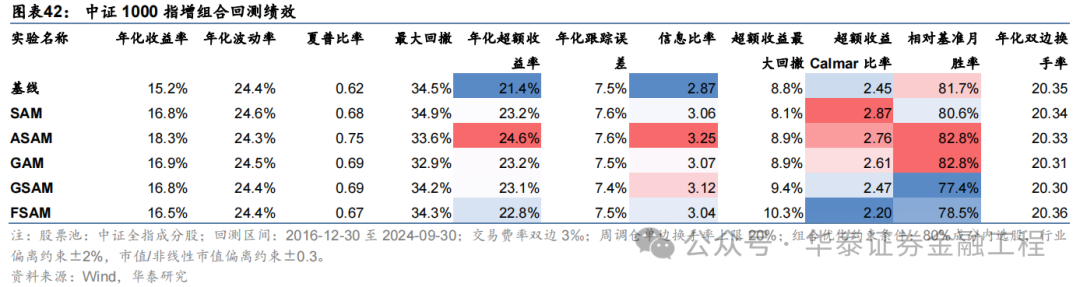
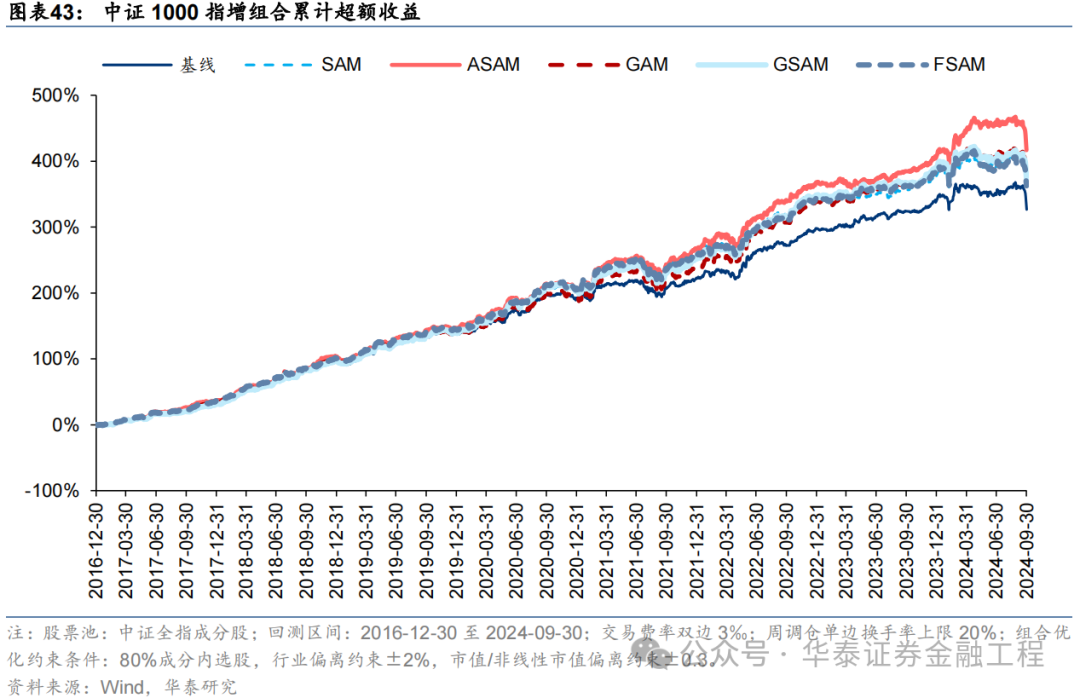
中证1000增强组合

基于6组实验预计因子构建的中证1000指数增强组合回测扫尾如下。测试扫尾标明，SAM优化器模子在年化逾额收益和信息比率方针上相对基线模子均有明显上风，可将年化逾额收益栽培2%，信息比率栽培0.2驾驭。其中从逾额收益及信息比率角度看表现最好的模子为ASAM，可将年化逾额收益从21.4%栽培至24.6%，信息比率从2.87栽培至3.25。

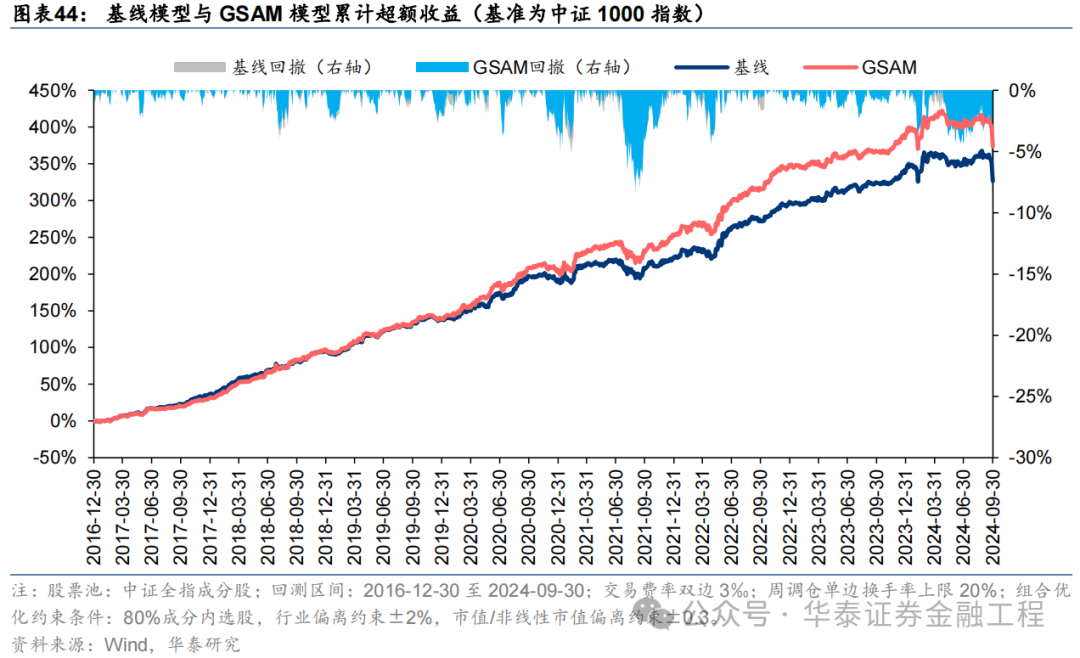
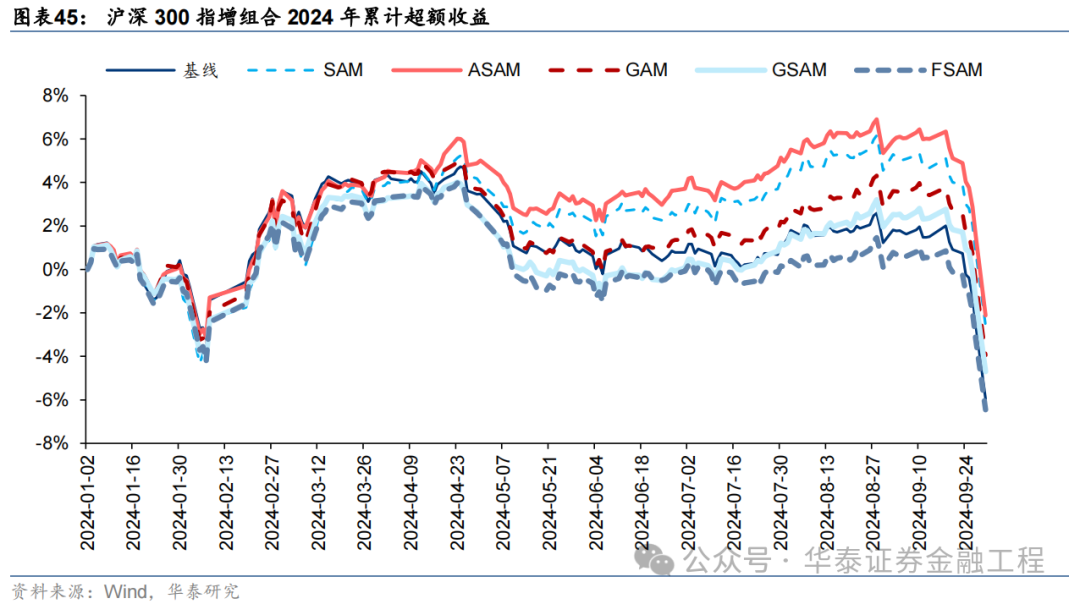
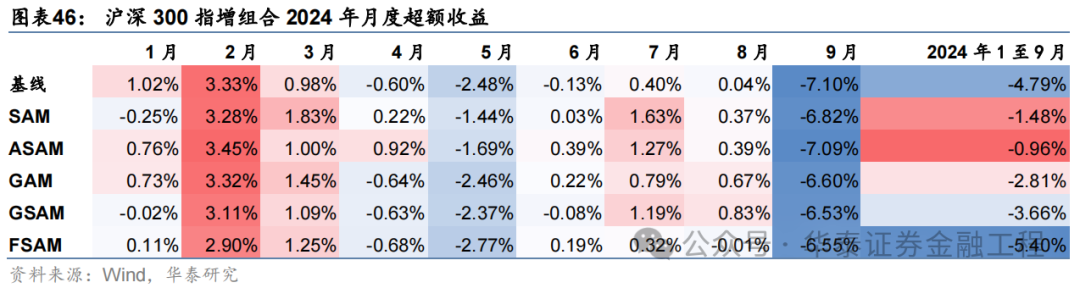
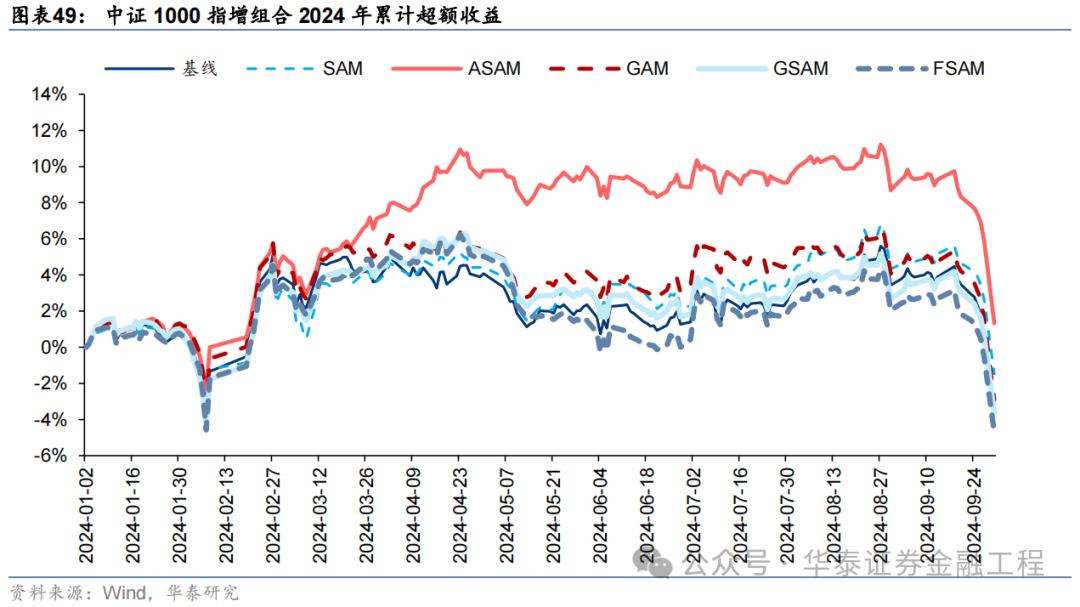
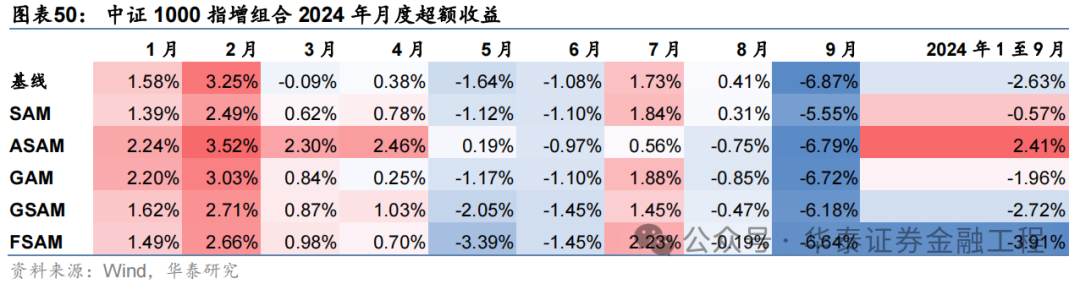
2024年功绩表现

统计各指增组合2024年以来功绩表现如下。分析发现，各指增组合在2024年9月末的大幅波动下逾额收益均迎来显赫回撤。但SAM模子偏执创新模子相对基线模子均具有雄厚上风。其中ASAM模子在2024年表现凸起，三组指增功绩均排行第一，且逾额收益首先基线模子约5%。

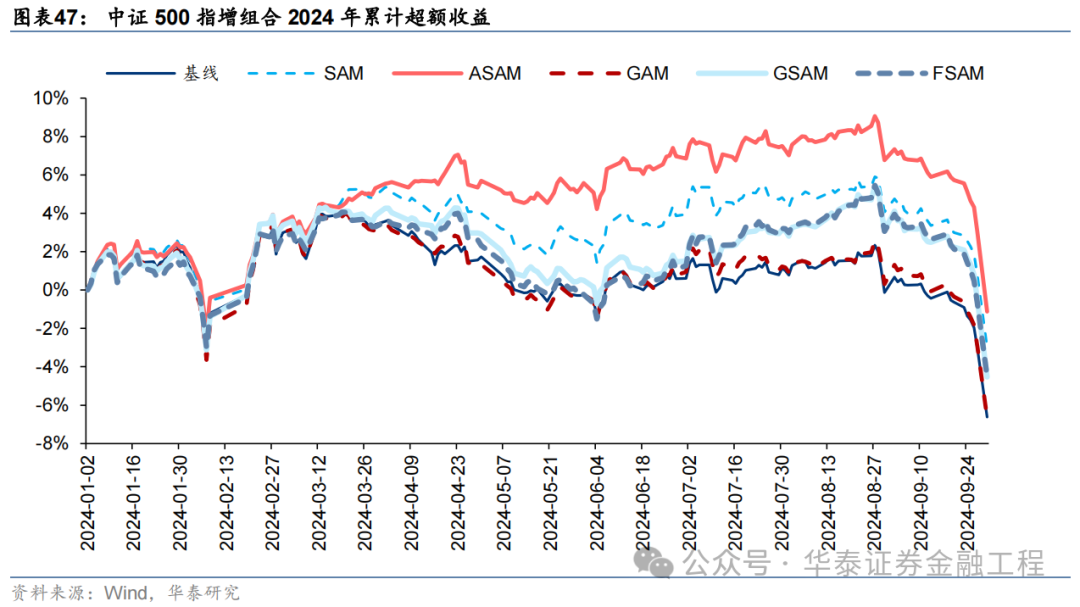
05 追究

本辩论先容一种低资本、高通用性的正则化步伐Sharpness Aware Minimization（SAM），从优化器的角度栽培模子的泛化性能。本文首先综述各种正则化步伐在改善模子泛化性能中的遑急性，其次分析SAM优化器相较于传统优化器的创新偏执旨趣，接着先容学术界对SAM优化器的进一步创新，终末以端到端的GRU量价因子挖掘模子当作基线模子，编削教师模子使用的优化器进行实证。扫尾标明应用SAM优化器能有用欺压模子过拟合，显赫栽培模子预计因子的多头端收益，且基于各SAM模子构建的指数增强组合功绩均显赫优于基线模子。

SAM优化器通过追求“平坦极小值”，增强模子鲁棒性。SGD、Adam等传统优化器进行梯度下跌时仅以最小化亏本函数值为方针，易落入“浓烈极小值”，导致模子其对输入数据散播敏锐度高，泛化性能较差。SAM优化器将亏本函数的平坦度加入优化方针，不仅最小化亏本函数值，同期最小化模子权要点隔邻亏本函数的变化幅度，使优化后模子权重处于一个平坦的极小值处，加多了模子的鲁棒性。基于SAM优化器，ASAM、GSAM等创新算法被陆续建议，从参数圭臬自适合性、扰动标的的准确性等方面进一步增强了SAM优化器的性能。

SAM优化器能镌汰教师过程中的过拟合，栽培模子的泛化性能。SAM优化器想象初志是使模子教师时在权重空间中找到一条简易的旅途进行梯度下跌，改善模子权重空间的平坦度。可通过不雅察模子教师过程中评价方针的变化趋势以及亏本函数地形图对其进行考据。从评价方针的变化趋势分析，SAM模子在考据集上IC、IR方针下跌幅度较缓，教师过程中评价方针最大值均高于基线模子；从亏本函数地形分析，SAM模子在教师集上亏本函数地形相较基线模子愈加平坦，测试集上亏本函数值举座更低。抽象两者，SAM优化器能有用欺压教师过程中的过拟合，栽培模子的泛化性能。

SAM优化器能显赫栽培AI量化模子表现。本辩论基于GRU模子，对比AdamW优化器与各种SAM优化器模子表现。从预计因子表现看，SAM优化器能栽培因子多头收益；从指数增强组合功绩看，SAM模子偏执创新版块模子在三组指数增强组合功绩均显赫优于基线模子。2016-12-30至2024-09-30内，抽象表现最好模子为GSAM模子，单因子回测TOP层年化逾额收益高于31%，沪深300、中证500和中证1000增强组合年化逾额收益永别为10.9%、15.1%和23.1%，信息比率永别为1.87、2.26和3.12，显赫优于基线模子。2024年以来ASAM模子表现凸起，三组指数增强组合逾额收益均首先基线模子约5%。

本辩论仍存在以下未尽之处：

本辩论测试SAM模子均采用文件中推选参数，并未针对AI量化模子作念大领域参数调优；

本辩论仅对SAM优化器的性能创新版块优化器进行测试，未对效用创新版块的优化器进行测试。SAM优化器在教师时需要进行两次梯度下跌，由此会带来一定的稀奇野心资本，对SAM优化器的效用进行创新有望栽培AI量化模子的教师效用；

本辩论对各创新版块的SAM优化器进行单独测试，后续辩论中可尝试纠合各种创新标的，得到一个抽象创新版块的SAM优化器。

参考文件

Kwon, J., Kim, J., Park, H., Choi, I.K., 2021. ASAM: Adaptive Sharpness-Aware Minimization for Scale-Invariant Learning of Deep Neural Networks, in: Proceedings of the 38th International Conference on Machine Learning. Presented at the International Conference on Machine Learning, PMLR, pp. 5905–5914.

Sun, Y., Shen, L., Chen, S., Ding, L., Tao, D., 2023. Dynamic Regularized Sharpness Aware Minimization in Federated Learning: Approaching Global Consistency and Smooth Landscape, in: Proceedings of the 40th International Conference on Machine Learning. Presented at the International Conference on Machine Learning, PMLR, pp. 32991–33013.

Li, T., Yan, W., Lei, Z., Wu, Y., Fang, K., Yang, M., Huang, X., 2022. Efficient Generalization Improvement Guided by Random Weight Perturbation.

Du, J., Yan, H., Feng, J., Zhou, J.T., Zhen, L., Goh, R.S.M., Tan, V.Y.F., 2022. Efficient Sharpness-aware Minimization for Improved Training of Neural Networks.

Li, T., Zhou, P., He, Z., Cheng, X., Huang, X., 2024. Friendly Sharpness-Aware Minimization. Presented at the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 5631–5640.

Zhang, X., Xu, R., Yu, H., Zou, H., Cui, P., 2023. Gradient Norm Aware Minimization Seeks First-Order Flatness and Improves Generalization. Presented at the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 20247–20257.

Mi, P., Shen, L., Ren, T., Zhou, Y., Sun, X., Ji, R., Tao, D., 2022. Make Sharpness-Aware Minimization Stronger: A Sparsified Perturbation Approach.

Zhao, Y., Zhang, H., Hu, X., 2023. Randomized Sharpness-Aware Training for Boosting Computational Efficiency in Deep Learning.

Foret, P., Kleiner, A., Mobahi, H., Neyshabur, B., 2021. Sharpness-Aware Minimization for Efficiently Improving Generalization.

Du, J., Zhou, D., Feng, J., Tan, V., Zhou, J.T., 2022. Sharpness-Aware Training for Free. Advances in Neural Information Processing Systems 35, 23439–23451.

Zhuang, J., Gong, B., Yuan, L., Cui, Y., Adam, H., Dvornek, N., Tatikonda, S., Duncan, J., Liu, T., 2022. Surrogate Gap Minimization Improves Sharpness-Aware Training.

Liu, Y., Mai, S., Chen, X., Hsieh, C.-J., You, Y., 2022. Towards Efficient and Scalable Sharpness-Aware Minimization. Presented at the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 12360–12370.

Li, H., Xu, Z., Taylor, G., Studer, C., Goldstein, T., 2018. Visualizing the Loss Landscape of Neural Nets, in: Advances in Neural Information Processing Systems. Curran Associates, Inc.

风险提醒：

东谈主工智能挖掘阛阓轨则是对历史的追究，阛阓轨则在将来可能失效。深度学习模子受立地数影响较大。本文回测假设以vwap价钱成交，未研讨其他影响往返因素。